No program is an island

One of the first things you notice when you start either Maxima or Octave is that these programs run on a character-based terminal. It doesn't matter if you have the state of the art graphical user interface on Mac OS X, Linux or Windows, they will take input in the form of written commands and will display their results as strings of ASCII characters. This is not a bad thing in itself, it just shows that they have a lot of history behind them, especially Maxima. Make no mistake, these programs are very sophisticated and implement algorithms that incorporate a vast repository of mathematical knowledge.

In order to overcome their UI shortcomings, Maxima and Octave today are augmented with other programs that are well integrated in the graphical environments of modern operating systems. There are two categories of such helper programs.

The first one is the Integrated Development Environment (IDE). This is a replacement for the character terminal as the main interface with the program. Although the command line is still available, some commands can be activated by pushing buttons or clicking menus. Besides, you have a text editor for editing scripts, integrated online help and many other niceties. This concept, of course, is not new. It has been around at least since the early days of Visual Basic and Turbo Pascal. To be fair, even Emacs had such an integrated environment earlier than that, although not in a graphical environment. For Maxima, one usually uses wxMaxima while for Octave, QtOctave is a common choice.

The second category of helper program is the plotting utility. Although some IDEs can also graph functions, curves and surfaces, this task is usually relegated to a specialized program. There are some possible choices here (see the List of information graphics software in my previous post) but both Maxima and Octave use the services of Gnuplot.

But the story doesn't end here! Gnuplot itself does not know everything about graphical environments so it relies on yet other programs to do the low level display. The list of output devices is long, ranging from real graphical terminals to terminal emulators that run on top of graphical environments. If you're running on Linux, for example, XTerm comes up naturally, but on Mac OS X your best choice would probably be AquaTerm, which incorporates the native Mac look and feel. In some cases you might use one of these terminals to interactively work on a problem until you are satisfied with the resulting graphic. Then, if you want to publish it, you could output it directly into a file in a format that supports graphics, such as Encapsulated PostScript (.eps), Portable Document Format (.pdf) and others.


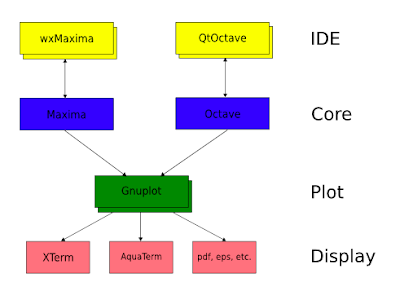
This architecture of interconnected programs is not new either. It more or less follows the early Unix motto that said that each program should do one thing well and one thing only. Nobody would think that Maxima and Octave do one thing only, but you can think of this rationale in a new level, where they do the core computations and other specialized programs do the input and output.

Now, as Monk would put it, this is a curse and a blessing. It's a curse for newcomers because they don't get a unified view of the program they're trying to use. Instead, they see a many headed beast that can be hard to correctly install, configure and understand. It also introduces new points of failure and makes it harder to keep all modules up to date in a compatible fashion.

The levels of complexity can run even deeper. When you run Maxima, for example, you don't see any process with this name (or similar). Maxima is written in Lisp so what you see is a Lisp interpreter which is executing the Maxima code. Which Lisp? Well, as you might guess, there are many implementations that can do the job.

On the other hand, for the experienced user it's a blessing, because he or she can, to a certain extent, pick and choose the best modules for each task. In part, it is this extreme flexibility that has attracted so many people to the world of Free and Open Source Software (FOSS).

Broadening the Horizon

In my previous post I superficially compared the most evident math programs from the commercial and free/open source fronts. Evidently, I was aware that such a small sample was not comprehensive but I was surprised when I found out how small that sample really was.

While searching Wikipedia for math related software I came across several interesting items. You will find, for example, good descriptions of all the packages we talked about, but what really caught my attention were three pages comparing the main features of a large number of programs. I think it would be rather difficult for a single person to collect all this information, sort out the details and display everything nicely in a table, not to mention keeping all the entries up to date. This is a true community effort!

The first page compares programs that can manipulate mathematical expressions symbolically. These are now called "Computer Algebra Systems" (CAS) and are epitomized by Macsyma:

Comparison of computer algebra systems

The second page is about numerical software. There is, of course, a lot of overlapping between these two categories (and the third one below), but the prototypical example here is Octave:

Comparison of numerical analysis software

Finally, this third page concentrates on programs that can create graphics. Again the overlap is big, but there is a table specifically comparing plotting programs, where our favorite example would be Gnuplot:

List of information graphics software

I'm sure there are many more programs out there that didn't enter these lists, either because they are too specialized or because they haven't reached maturity yet. Anyway, the landscape of math programs presented by Wikipedia is much wider than the one I painted last time!

Mathematical Software

So we want to experiment with mathematical software. At this stage we don't have any specific goal in mind. We just want to explore the possibilities and play with some programs a bit. We would like to do numerical calculations and also to evaluate symbolic expressions: factor, expand, integrate and differentiate. Finally, we would like to display the results of this work graphically. How easily can we plot curves and surfaces? How about data sets?

The commercial landscape for mathematical software is relatively small. It is basically dominated by two heavy weights: Mathematica and MATLAB. The first is the all-in-one solution to scientific computing. It can do numerics, symbolics, graphics and programming. The second, while probably equally capable, is seen as more oriented to matrix and numerical calculations. In a second tier, if you will, one finds two other strong contenders: Maple and Mathcad. Like their more famous friends these products can also be extended via numerous add-ons and packages to accommodate specific engineering and scientific needs.

In a third tier, considerably lower than the above products, one should not forget the ubiquitous Excel. Although we tend to associate this name to price lists and accounting, a spreadsheet can handle some interesting scientific tasks. I don't think you can evaluate symbolic expressions with Excel but you can do statistics, numerical integration and differentiation and, of course, draw nice graphics.

Judging by the existing literature about them, these commercial products are enormously successful. Each has a large number of users and (with the exception of Excel) could be used for learning and experimenting with mathematics. The problem, as we all know, is that they are also very, very expensive. Moreover, if you are curious about how they implement this or that function, you are out of luck. These products don't come with source code and you can only guess which techniques they use to implement your favorite feature.

So, without the need of further explaining, let's look at the Free/Open Software options!

Just a little searching around is necessary to reveal the two most famous mathematical programs in the free software world: Maxima and Octave. Perhaps I should put Octave first, given that it seems to be much more popular than Maxima, but I want to emphasize that they more or less mimic their commercial counterparts Mathematica and MATLAB.

Saying that Maxima tries to mimic Mathematica is, of course, a misstatement. Maxima descends from Macsyma, which takes its name not from the Apple computer but from the famous MIT Project MAC of the 60's, and as such is the granddaddy of all mathematical software. The "syma" suffix, as you may guess, suggests that this program was intended to do symbolic math, a revolutionary feature at that time. Mathematica has no direct link to Macsyma except, perhaps, as a source of inspiration. So the relation between these programs is rather tenuous but I think that today Maxima is still the closest free alternative to Mathematica.

On the other hand, Octave tries hard to emulate MATLAB in many areas. I'm still a newcomer to Octave, but a quick glimpse at its manual shows its authors' concerns about compatibility with the commercial cousin. There seem to be some small restrictions but the core functionality of MATLAB seems to be available in Octave. As "Macsyma", the name "Octave" is a bit misleading. It has nothing to do with music but comes, as we learn by reading the first paragraphs of its documentation, from a Professor close to the original author!

In the next posts I will try to report my own experiences dealing with these free mathematical programs and some other helper packages like gnuplot.