Plotting with Maxima

Maxima is about computation, mainly symbolic computation. However, when you talk about math software, the first thing that comes to the mind of most people are beautifully rendered 3-D surfaces. The prototypical image is the sombrero-like surface you see below.


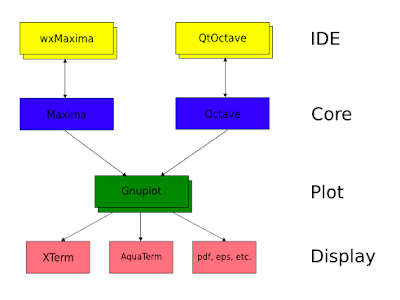
I've added it here just as an eye-catcher, because that's not where I want to begin. I'd like to start exploring the plot commands in Maxima with something simpler, but not as simple as the usual sines, cosines and polynomials. I wanted something a bit more challenging and at the same time related to a real problem. After searching for a while I came across Plank's Law, which every physics student studies in his or her first class of Quantum Mechanics.

Plank's Law gives the black-body radiation as a function of temperature and either frequency or wavelength. It can be expressed in a few different ways, depending on whether you want the density per solid angle or the total energy. This last form is commonly expressed as

You can find a good plot of this function for various temperatures in the Wikipedia article about Plank's Law, here.

So how do we go about plotting it with Maxima? There are basically two aspects to it. First you must encode the equation in a way that Maxima will understand. In other words, you must code it using Maxima's syntax. Second, you must use the plot2d command giving it proper arguments so that it can perform its job.

Instead of giving you the final result, I think it's more interesting if I tell you about some of my attempts and their gradual improvements. So we will do it in three steps.

Maxima functions and definitions can be kept in text files and loaded as needed with the "batch()" function. I keep a small batch file with the definitions of useful physical constants. In this example we will need

c: 2.9979e8$ /* Speed of light */
h: 6.6256e-34$ /* Plank's constant */
k: 1.3805e-23$ /* Boltzmann's constant */

You use ":" to separate a variable's name from its initial value. In this case the variables will actually be constants.

In a separate file I entered my first attempt:

/* First attempt at Planck's law */
/* Helper constants */
k1: 8 * %pi * h * c$
k2: (h * c) / k$

/* Function definition */
E(l,T) := k1 * (l ^ -5) * (1 / (exp(k2/(l * T)) - 1))$

/* Plot command */
plot2d(E(l,5500),[l,100e-9,2000e-9])$

Note that I defined two auxiliary constants, k1 and k2. Not only do they make the equation look simpler but they also avoid some unnecessary computation. Remember that Maxima will use the formula we give it to calculate the function's value in a range of very close points. So using these pre-calculated constants it won't need to calculate them over and over again for each point in the x-axis.

A few observations about the function definition. First note that it uses ":=" instead of ":" as we did for variables. Second, exponentiation is denoted by "^". It would have been nice to use the character lambda instead of the lowercase "l" and have wxMaxima display it as a Greek character, but I don't know how to do this. Maxima and wxMaxima do this nicely for other Greek letters, like alpha and theta, but somehow it does not work for lambda. Finally, operator precedence can be tricky so it's safer to use parentheses when in doubt.

As for the plot2d command, in its simpler form it takes two arguments. The first one is the expression we want to plot and the second one is the range of the independent variable. So we are asking it to plot the Energy at temperature T=5500K, for lambda varying from 100 to 2000 nm.

This was the resulting plot:


Not bad for a first try! Note that Maxima automatically scales the vertical axis so that the whole graph fits in, but the units for both axes are somewhat cryptic. In our second attempt we will try to display more friendly axes. Here's the improved code:

/* Second attempt at Planck's law */
/* Helper constants */
k1: 8 * %pi * h * c * 1e-3$
k2: (h * c) / k$

/* Function definition */
E(l,T) := k1 * ((l * 1e-9) ^ -5) *
(1 / (exp(k2/((l * 1e-9) * T)) - 1))$

/* Plot command */
plot2d(E(l,5500),
[l,100,2000],
[xlabel,"lambda [nm]"],
[ylabel,"E(lambda) [kJ/nm]"])$

In order to make the vertical axis look like the one in the graph from the Wikipedia page we have scaled the k1 constant by 1000. And since we want the horizontal axis to be in units of nm, we added the factor 1 x 10^-9 to each occurrence of lambda in the formula. Note the small quirk in Maxima's syntax. It uses the letter "e" to denote constants multiplied by a power of ten but uses a different symbol, "^", to denote exponentiation in expressions. No big deal, this is actually used in most (all?) programming languages, but it does look strange from a mathematical notation point of view.

Finally, we added some more arguments to the plot2d() command. They are the plotting options and take the form of lists enclosed by square brackets in which the first element is the option name. For this example we just attached labels to each of the axes, displaying their meaning and units. Here's the result:

We might say that we have accomplished our initial goal, at least for a single temperature. What remains to be done is add more temperatures, each in a different color. This will be very easy, since, for our convenience, the plot2d() commands accepts a list of expressions to plot as its first argument! So far we have given it a single expression, viz. E(l,5500), but now we will give it a list: [E(L,3500),E(L,4000),E(L,4500),E(L,5000),E(L,5500)]. Here I started using uppercase "L" for lambda because the lowercase version could be easily mistaken by the digit 1.

/* Final version of Planck's law plot */
/* Helper constants */
k1: 8 * %pi * h * c * 1e-3$
k2: (h * c) / k$

/* Function definition */
E(L,T) := k1 * ((L * 1e-9) ^ -5) *
(1 / (exp(k2/((L * 1e-9) * T)) - 1))$

/* Plot command */
plot2d([E(L,3500),E(L,4000),E(L,4500),E(L,5000),E(L,5500)],
[L,100,2000],
[xlabel,"lambda [nm]"],
[ylabel,"E(lambda) [kJ/nm]"],
[color,black,cyan,blue,green,red],
[legend,"T=3500K","T=4000K","T=4500K","T=5000K","T=5500K"]);

Besides, I have added more options to plot2d(). We now specify which colors are to be used for each plotted expression and which legend to attach to it. Unfortunately the legend does not appear near the plot but on the right-hand upper corner. So here's the final result:


Ok, so now I'm satisfied. This was a good exercise and the result looks very much like the plot from Wikipedia. But wait! E(L,T) is obviously a two-variable function although we have been using it like a single variable function by choosing only a few fixed values for the temperature. This is like a contour map of a 3D surface. We can do better. We can use Maxima's plot3d() command to have a continuous view of the Energy function for a range of temperatures! Here's how we do it:

plot3d(E(L,T),
[L,100,2000],
[T,1500,5500],
[zlabel,"E(L,T)"],
[legend,"Spectral Energy Density"],
[grid,50,50]);

It's really that simple! We just added a new axis label and the grid option to make the surface look smoother (although that was not necessary). Here's how it looks:


I had never seen Planck's function plotted like this. I guess the plotting software available around 1900, when Planck created it, was only capable of doing 2-D plots :-) This 3-D plot gave me a new insight into the problem. I immediately saw that the energy is not bounded by the temperature. When you look at the 2-D contour plot, perhaps you could overlook the fact that temperature can increase more and more and that the energy goes the same way. Not so in the 3-D plot, where temperature is one of the axes!

By the way, the sombrero plot of the beginning of this post was done with

plot3d(cos(x^2+y^2)*exp(-(x^2+y^2)/5),
[x,-4,4],
[y,-4,4],
[grid,100,100]);

The Grand Design

The Grand Design
Stephen Hawking
Leonard Mlodinow
Kindle Edition



Although Hawking's name features more prominently on the cover than Mlodinow's, I cannot help fantasizing about how the work division was done. It is not difficult to imagine that Hawking is basically the author of the last chapter, which carries the same title as the book itself, while Mlodinow did the hard work of writing all the other 7 chapters. Hawking was probably also the guiding hand that made sure the thread developed in these initial chapters would carefully lead the reader to his own conclusion. And, of course, he's probably responsible for the typically Pythonesque humor sprinkled throughout the text.

The first chapters take the reader through an accelerated account of the progress of humankind's understanding of nature. It starts with the Greek thinkers, skips the middle ages, jumps to Copernicus and Galileo, follows to Newton and finally gets to Einstein and his theory of General Relativity. It also covers the development of quantum physics in the early decades of the 20th century and the fruitless attempts to unite it peacefully with GR. Finally the authors tell how this lead to string theory and later M-Theory and why it remains the best candidate to explain nature at a deeper level. The facts and theories are up to date (as of 2010), but there's not much new material there, nothing that a reader of "The Universe in a Nutshell" already didn't know.

Although these chapters cover standard material as seen in other popular science books, there are two things that make them worth reading. First is the concept of model-dependent realism, which is a retreat from the popular credo of the 80's and 90's in a Theory of Everything. Instead, this concept admits that reality cannot be modeled by a single theory but needs a family of them to model different aspects. The second thing is the more philosophical slant of the text. While most scientists would not like to address these issues, leaving them to philosophers, the authors state right at the beginning of the book that they want to know the answer to these questions:

- Why is there something rather than nothing?
- Why do we exist?
- Why this particular set of laws (of physics) and not some other?

As you can see, these are grandiose questions (could they be more so?) and I won't spoil your pleasure of reading this nice book to find the answers yourself. However, as you might suspect, they don't involve the concept of God and none of them is 42!

One final comment about how I "weighed" the chapters. I read this book on a Kindle and I like to use its ability to highlight pieces of text. This is basically what you would do with a yellow pen in a dead-tree book, with the advantage that you can see all of your highlights in a single place if you want. In the initial chapters I kept an average of 2 or 3 highlights per chapter. However, when I reached the "Grand Design" chapter in the end, I found myself marking almost everything. This showed me that this was really a different chapter, with much more new content than the others.

Whatever your background, I think everybody is interested in the profound questions that this books addresses. The answers that Hawking and Mlodinow give are not easy to swallow, but they are courageous and deserve careful consideration.

Learning to Use Tensors in Maxima

In my previous post I used Maxima to derive the metric tensor of the 3-sphere using the coordinate system described by Mathview in his YouTube video. Now I'd like to continue exploring Maxima to calculate various other properties of S^3.

In a follow up video where he calculated the Christofell symbols for the 3-sphere, Mathview used new coordinate transformations that give a right-handed coordinate system instead of a left-handed one as in his previous video. It is very similar to the original, the difference being just the choice of the 3rd angle, theta3. This small change greatly simplifies the metric tensor and, as a consequence, all other derived tensors and properties. You can follow his derivation in the video below.

How do I get the Christoffel Symbols on the 3-Sphere?



Last time I used just the basic facilities of Maxima to derive the metric tensor from the transformations. I then said that it would be nice, in the future, to use one of the tensor packages that comes with Maxima to redo those calculations. Today I found out that you can start from the coordinate transformations and go directly to the metric, Christofells and other tensors. However, we can plug in the output of my original method into the ctensor package and continue from there. Although this gives a little more work it is more pedagogical as it reveals some of the details of how tensors are handled by this package.

So here we will quickly repeat the derivation of the metric tensor, only now using Mathview's new coordinate system. We assign the final matrix to "lg", for "lower-indices g". Maxima uses this convention to name some of the variables that it uses to hold tensors. The first letter in the name can be "l", "u" or "m" for lower, upper or mixed indices respectively.



I don't know why g[2,2] came out with (1 - sin(theta[3])^2) instead of cos(theta[3])^2. I tried other simplification functions but none did this transformation so I ended up doing it by hand.

Next we calculate ug, the inverse of lg, as it will also be needed.



Maxima comes with two packages that handle tensors: itensor and ctensor. The former does indicial tensor manipulation and the latter does component manipulation. ctensor is sometimes also referred to as the "curved space" tensor package. This is the one we want!

As I said, ctensor has a way to allow you to start directly from the coordinate transformations (ct_coordsys()). There is also a dialog based function that asks for the various components of the metric tensor (csetup()). But we have already calculated the metric tensor by our own device and the choice of names "lg" and "ug" was no accident: they are exactly what ctensor expects.

At this point we can see that Maxima implements component tensors as regular multi-dimensional arrays: [n,n] arrays (matrices) for rank 2 tensors, [n,n,n] arrays for rank 3 tensors and so on up to rank 5. Another interesting observation is that ctensor is not built in Maxima, but rather, it's a loadable package. In other words, it's implemented in the Maxima programming language, not in Lisp.

Therefore, we next load ctensor and give it the missing information it needs to do its calculations: the number of dimensions we'll be working on and a list of the variables that hold the coordinates.



Now we're ready for the fun! Equipped with the metric tensor and the list of variable names, ctensor can easily calculate the Christofell symbols, the Ricci tensor and many others. We'll start with the Christofell symbols of the 1st kind, which ctensor names as "lcs" because all the indices are downstairs:



Some observations are needed here. First, note that ctensor displays only the non-zero, unique elements in lcs[i,j,k]. In this exercise there are 6 non-zero elements, but only 4 are unique. The other two are duplicates due to the symmetry of lcs[]. Second, the convention that Mathview uses for the indices is different from the one used by Maxima. To convert between Mathview and Maxima, just reverse the order of the indices. So, what Mathview calls Gamma(3,1,1) is the same as lcs[1,1,3] which is -cos(theta[3]) * sin(theta[3]) * a^2. Finally, it's a pity that wxMaxima displays the Christofell symbols this way. It would have been nicer to use the proper Gamma character!

Now, just for fun we calculate the Christoffell symbols of the second kind (mcs), the Ricci tensor and the Riemann curvature tensor.



This post shows but a small portion of the capabilities of ctensor and Maxima. There are dozens of other interesting functions that you can learn about by reading the manual. Although there's no doubt about the power of Maxima for manipulating tensors, students learning the subject should make sure to go over the whole process of calculating the Christofell symbols and the Ricci and Riemann tensors by hand a few times. By watching Mathview's videos you'll see how much more insight this approach gives you as opposed to just seeing Maxima spit out the answers!

Turning the digital crank

Mathview has a series of very interesting videos on YouTube about Differential Geometry and related topics. In one of these videos he attacks the problem of finding the metric tensor for the 3-sphere using as coordinates a set of 3 orthogonal angles and a radius. Here's the first part of the video:

What's the Metric Tensor of the 3-Sphere?



This is a good exercise for those learning the subject as it gives us the opportunity to apply the theory to a concrete example. Of course, working with S^3 is not the best example of concrete mathematics because it requires dealing with 4 dimensions, but you know what I mean. Besides, the 3-sphere received a lot of attention lately due to the proof of the Poincaré Conjecture by Perelman.

The exercise is not intrinsically difficult, but it involves a lot of calculations in the form or partial derivatives and trigonometric simplifications. It is very easy to eat a minus sign here or use a sin(x) where cos(x) was meant and wreck the whole thing. Since this is basically a mechanical process, Mathview calls it "turning the crank".

Since I'm learning to use Maxima, which has powerful symbolic manipulation features, I thought it might be a good idea to exercise it trying to verify Mathview's result for the S^3 metric tensor. In other words, I'd like to "turn the crank" the digital way. I must say that it took me many hours to put all the pieces together, but in the end it was well worth the effort. Not only did I verify that Mathview's result was correct (not that I doubted it :-) but I also learned a few interesting things about Maxima.

I wanted to Read The Fine Manual entirely but that seemed like a bad idea since it's very large (900+ pages) and has lots of specialized packages that are not of my concern for now. Therefore I just skimmed over the main topics and tried to extract what I needed for this job. I immediately saw that it has a tensor package which knows about the metric tensor, Christofell symbols, etc. However, that was too complicated for a first encounter with Maxima, so I just used its generic features. As I learn more about Maxima I may revisit this exercise and try to do it with the itensor/ctensor packages.

We start by defining how the Cartesian coordinates relate to the polar coordinates. These relations were derived by Mathview at the beginning of his video. Moving from 3D to 4D with an orthogonal angle was a nice trick! Then we define an array 'X' with these definitions.



Two things to note here. First, Maxima knows about Greek letters like "theta" and wxMaxima (the GUI) renders them nicely as one would see in a well typeset book. Second, the square brackets used to denote the indices are transformed into subscripts, also as we would expect. We must use this notation here as it will allow us to refer to these variables generically via their indices.

As a first test, let's find the derivative of X with respect to theta1:



Now we define the metric tensor. It's the dot product of the partial derivatives of the coordinates. In this case we're only interested in the angles, so we leave out the radius, which we take to be constant (say, 1).



Note that this is not yet the tensor. It's just a "matrix function". For instance, if we want to know a particular element, it can be evaluated:



Here we learned that Maxima does not perform all the simplifications when presenting its results. Depending on what kind of calculations you're doing, there are different simplification functions and strategies. In our case, "trigsimp" did the trick and transformed that long trigonometric expression into r^2.

Finally, in order to create the g matrix we use "genmatrix", which will apply the function to all the indices. The result was not in a simplified form, but applying trigsimp after that reduced the matrix to the form that Mathview derived by hand!



I hope this has been a small but interesting introduction to Maxima. In future posts I will continue exploring it.

No program is an island

One of the first things you notice when you start either Maxima or Octave is that these programs run on a character-based terminal. It doesn't matter if you have the state of the art graphical user interface on Mac OS X, Linux or Windows, they will take input in the form of written commands and will display their results as strings of ASCII characters. This is not a bad thing in itself, it just shows that they have a lot of history behind them, especially Maxima. Make no mistake, these programs are very sophisticated and implement algorithms that incorporate a vast repository of mathematical knowledge.

In order to overcome their UI shortcomings, Maxima and Octave today are augmented with other programs that are well integrated in the graphical environments of modern operating systems. There are two categories of such helper programs.

The first one is the Integrated Development Environment (IDE). This is a replacement for the character terminal as the main interface with the program. Although the command line is still available, some commands can be activated by pushing buttons or clicking menus. Besides, you have a text editor for editing scripts, integrated online help and many other niceties. This concept, of course, is not new. It has been around at least since the early days of Visual Basic and Turbo Pascal. To be fair, even Emacs had such an integrated environment earlier than that, although not in a graphical environment. For Maxima, one usually uses wxMaxima while for Octave, QtOctave is a common choice.

The second category of helper program is the plotting utility. Although some IDEs can also graph functions, curves and surfaces, this task is usually relegated to a specialized program. There are some possible choices here (see the List of information graphics software in my previous post) but both Maxima and Octave use the services of Gnuplot.

But the story doesn't end here! Gnuplot itself does not know everything about graphical environments so it relies on yet other programs to do the low level display. The list of output devices is long, ranging from real graphical terminals to terminal emulators that run on top of graphical environments. If you're running on Linux, for example, XTerm comes up naturally, but on Mac OS X your best choice would probably be AquaTerm, which incorporates the native Mac look and feel. In some cases you might use one of these terminals to interactively work on a problem until you are satisfied with the resulting graphic. Then, if you want to publish it, you could output it directly into a file in a format that supports graphics, such as Encapsulated PostScript (.eps), Portable Document Format (.pdf) and others.


This architecture of interconnected programs is not new either. It more or less follows the early Unix motto that said that each program should do one thing well and one thing only. Nobody would think that Maxima and Octave do one thing only, but you can think of this rationale in a new level, where they do the core computations and other specialized programs do the input and output.

Now, as Monk would put it, this is a curse and a blessing. It's a curse for newcomers because they don't get a unified view of the program they're trying to use. Instead, they see a many headed beast that can be hard to correctly install, configure and understand. It also introduces new points of failure and makes it harder to keep all modules up to date in a compatible fashion.

The levels of complexity can run even deeper. When you run Maxima, for example, you don't see any process with this name (or similar). Maxima is written in Lisp so what you see is a Lisp interpreter which is executing the Maxima code. Which Lisp? Well, as you might guess, there are many implementations that can do the job.

On the other hand, for the experienced user it's a blessing, because he or she can, to a certain extent, pick and choose the best modules for each task. In part, it is this extreme flexibility that has attracted so many people to the world of Free and Open Source Software (FOSS).

Broadening the Horizon

In my previous post I superficially compared the most evident math programs from the commercial and free/open source fronts. Evidently, I was aware that such a small sample was not comprehensive but I was surprised when I found out how small that sample really was.

While searching Wikipedia for math related software I came across several interesting items. You will find, for example, good descriptions of all the packages we talked about, but what really caught my attention were three pages comparing the main features of a large number of programs. I think it would be rather difficult for a single person to collect all this information, sort out the details and display everything nicely in a table, not to mention keeping all the entries up to date. This is a true community effort!

The first page compares programs that can manipulate mathematical expressions symbolically. These are now called "Computer Algebra Systems" (CAS) and are epitomized by Macsyma:

Comparison of computer algebra systems

The second page is about numerical software. There is, of course, a lot of overlapping between these two categories (and the third one below), but the prototypical example here is Octave:

Comparison of numerical analysis software

Finally, this third page concentrates on programs that can create graphics. Again the overlap is big, but there is a table specifically comparing plotting programs, where our favorite example would be Gnuplot:

List of information graphics software

I'm sure there are many more programs out there that didn't enter these lists, either because they are too specialized or because they haven't reached maturity yet. Anyway, the landscape of math programs presented by Wikipedia is much wider than the one I painted last time!

Mathematical Software

So we want to experiment with mathematical software. At this stage we don't have any specific goal in mind. We just want to explore the possibilities and play with some programs a bit. We would like to do numerical calculations and also to evaluate symbolic expressions: factor, expand, integrate and differentiate. Finally, we would like to display the results of this work graphically. How easily can we plot curves and surfaces? How about data sets?

The commercial landscape for mathematical software is relatively small. It is basically dominated by two heavy weights: Mathematica and MATLAB. The first is the all-in-one solution to scientific computing. It can do numerics, symbolics, graphics and programming. The second, while probably equally capable, is seen as more oriented to matrix and numerical calculations. In a second tier, if you will, one finds two other strong contenders: Maple and Mathcad. Like their more famous friends these products can also be extended via numerous add-ons and packages to accommodate specific engineering and scientific needs.

In a third tier, considerably lower than the above products, one should not forget the ubiquitous Excel. Although we tend to associate this name to price lists and accounting, a spreadsheet can handle some interesting scientific tasks. I don't think you can evaluate symbolic expressions with Excel but you can do statistics, numerical integration and differentiation and, of course, draw nice graphics.

Judging by the existing literature about them, these commercial products are enormously successful. Each has a large number of users and (with the exception of Excel) could be used for learning and experimenting with mathematics. The problem, as we all know, is that they are also very, very expensive. Moreover, if you are curious about how they implement this or that function, you are out of luck. These products don't come with source code and you can only guess which techniques they use to implement your favorite feature.

So, without the need of further explaining, let's look at the Free/Open Software options!

Just a little searching around is necessary to reveal the two most famous mathematical programs in the free software world: Maxima and Octave. Perhaps I should put Octave first, given that it seems to be much more popular than Maxima, but I want to emphasize that they more or less mimic their commercial counterparts Mathematica and MATLAB.

Saying that Maxima tries to mimic Mathematica is, of course, a misstatement. Maxima descends from Macsyma, which takes its name not from the Apple computer but from the famous MIT Project MAC of the 60's, and as such is the granddaddy of all mathematical software. The "syma" suffix, as you may guess, suggests that this program was intended to do symbolic math, a revolutionary feature at that time. Mathematica has no direct link to Macsyma except, perhaps, as a source of inspiration. So the relation between these programs is rather tenuous but I think that today Maxima is still the closest free alternative to Mathematica.

On the other hand, Octave tries hard to emulate MATLAB in many areas. I'm still a newcomer to Octave, but a quick glimpse at its manual shows its authors' concerns about compatibility with the commercial cousin. There seem to be some small restrictions but the core functionality of MATLAB seems to be available in Octave. As "Macsyma", the name "Octave" is a bit misleading. It has nothing to do with music but comes, as we learn by reading the first paragraphs of its documentation, from a Professor close to the original author!

In the next posts I will try to report my own experiences dealing with these free mathematical programs and some other helper packages like gnuplot.